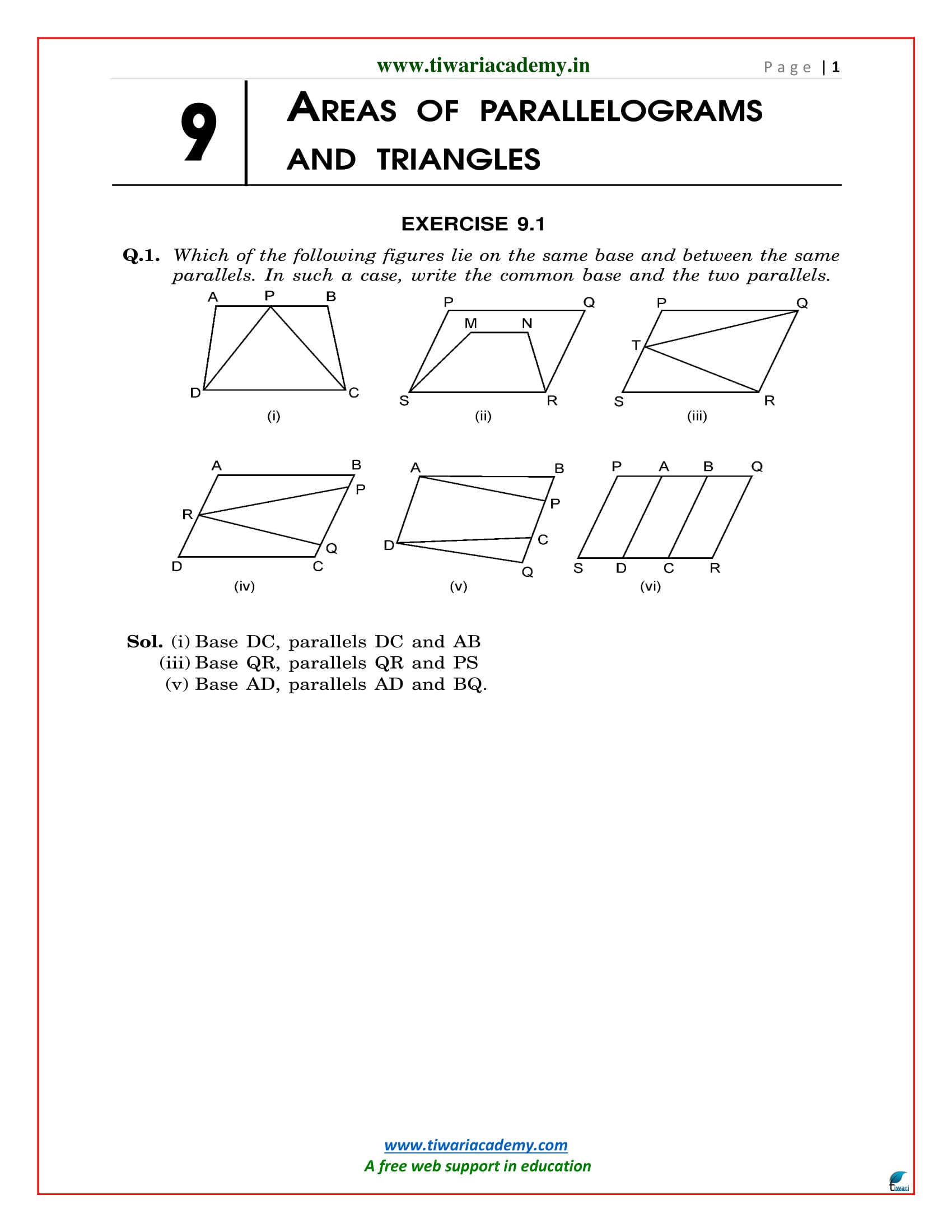
Download NCERT Solutions for Class 9 Maths Chapter 9 exercise 9.1 and 9.2 of areas of parallelograms and triangles in English Medium and Hindi Medium free to use. NCERT Solutions for class 9 Maths all chapters and NCERT Books are also given in downloadable form.
NCERT Solutions for Class 9 Maths Chapter 9
If you need solutions in Hindi, Click for Hindi Medium solutions of 9 Maths Chapter 9





9 Maths Chapter 9 All Exercises in Hindi
















To get the solutions in English, Click for English Medium solutions.
Class 9 Maths – Chapter 9 Important Questions
Areas of Parallelograms and Triangles
- Prove that the parallelograms on the same base and between same parallels are equal in area.
- Two triangles on the same base (or equal base) and between the same parallels are equal in area. Prove.
- Two triangles having the same base (or equal bases) and equal areas lies between the same parallels. Prove.
- PQRS is a Parallelograms and PQM is a triangle. If area of PQM = 18 cm2. Find the area of PQRS. [Answer: 36 cm2]
- In ∆ABC, AD is median. If area of ∆ABD=25 cm2 find the area of ∆ABC. [Answer: 50 cm2]
- If two parallelogram are on equal base and between the same parallels, then what is the ratio of their areas? [Answer: 1:1]
- A triangle and a Parallelograms are on the same base as well as between the same parallels then find the ratio of areas of triangle to that of the parallelogram. [Answer: 1:2]
- In ∆ABC, D, E, F are respectively the mid points of the sides AB, BC and AC. Find ratio of the area of ∆DEF and area of ∆ABC. [Answer: 1:4]
- If the base of a parallelogram is 8 cm and its altitude is 5 cm then find its area. [Answer: 40 cm2]
- If two triangles are on the same base and between the same parallels. Then find the ratio of area of the two triangles. [Answer: 1:1]
- Show that the median of a triangle divides it into two triangles of equal areas.
- P and Q are any two points lying on the side DC and AD respectively of a parallelogram ABCD. Show that ar(APB) = ar(BQC).
- If the ratio of altitude and area of the parallelogram is 2:11, then find the length of the base of parallelogram. [Answer: 11/2 units]
- AD is median of ∆ABC. If x is any point on AD Show that ar(∆ABX) = ar(∆ACX).
- M is any point on the median AD of ∆ABC. Show that ar(∆AMB) = ar(∆AMC).
- If D, E and F are respectively the mid points of sides BC, CA and AB of ∆ABC show that (i) BDEF is a parallelogram. (ii) ar(∆DEF) = 1/4 ar(∆ABC).
- ABCD is a trapezium in which the AB II DC. If diagonal AC and BD intersect at O. Prove that ar(∆AOD) = ar(∆BOC).
- ABCD is a parallelogram whose diagonals AC and BD intersect at O. A line through O intersects AB at P and DC at Q. Prove that: ar(∆ POA) = ar(∆ QOC).
- Diagonal PR and QS of quadrilateral PQRS intersect at T such that PT = TR and PS = QR. show than ar(∆PTS) = ar(∆RTQ).
- XY is a line parallel to side BC of a triangle ABC. If BE II AC and CF II AB meet XY at E and F respectively. Show that ar(∆ABE) = ar(∆ACF).
- If E, F, G and H are respectively the mid points of the sides of a parallelograms ABCD. Show that ar (EFGH) = 1/2ar(ABCD).
- A farmer has a square plot of land where the wants to grow five different crops at a time. On half of the area in the middle he want to grow rice but in rest four equal triangular parts he wants to grow different crops. a) Explain by diagram how he can divide the area to fulfil his purpose. b) By using the crop pattern which values are depicted by the farmer.